Concatenation process in DFA
Last Updated :
04 Jan, 2022
Prerequisite – Designing finite automata
Designing a DFA for the set of string over {a, b} such that string of the language start with “a” and end with “b”. There two desired language will be formed:
L1 = {a, aab, aabab, .......}
L2 = {b, bbab, bbabab, .......}
In L1, starting element is “a” and in L2, ending element is b.
State Transition Diagram for the language L1:
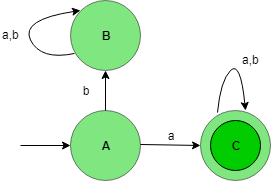
This DFA accepts all the string which starts with “a”. Here, state C is the final state and B is the dead state this is called so because after getting any alphabet this state will never go to final state.
State Transition Diagram for the language L2:

This DFA accepts all the string ending with alphabet “b”. Here, State B is called final state.
Now, Taking the concatenation of L1 and L2 language which gives the final result of the language which starts with “a” and end with “b”.
State Transition Diagram of L1.L2 i.e, L1 concat L2:
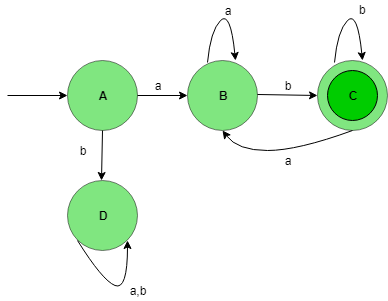
This DFA accept all the string which start with a and end with b. Here, State C is the final state and D is the dead state this is called so because after getting any input alphabet it will never go to final state.